The coastline paradox is a mathematical concept that describes the counterintuitive observation that the length of a coastline is not a fixed quantity, but rather depends on the scale at which it is measured. At smaller scales, more details of the coastline are revealed, resulting in a longer measured length. Conversely, at larger scales, many of these details are smoothed out, resulting in a shorter measured length.
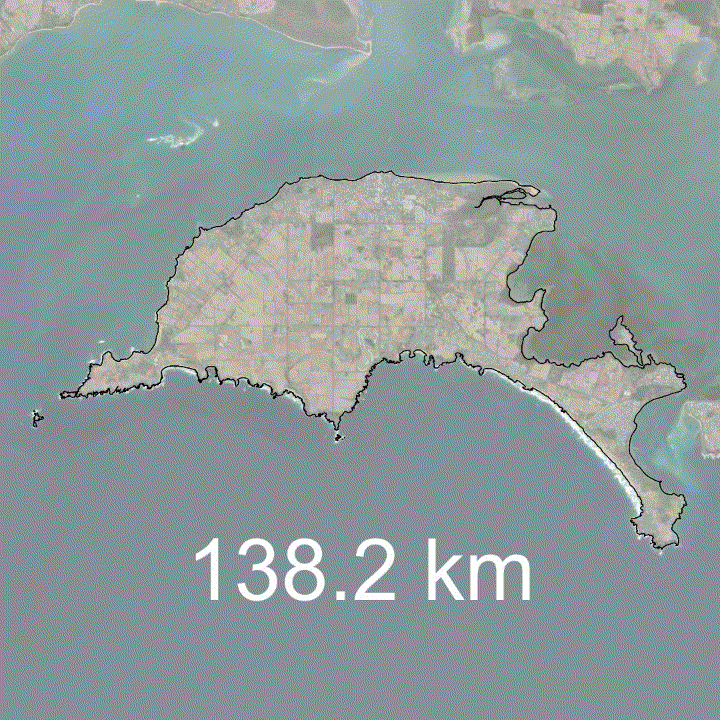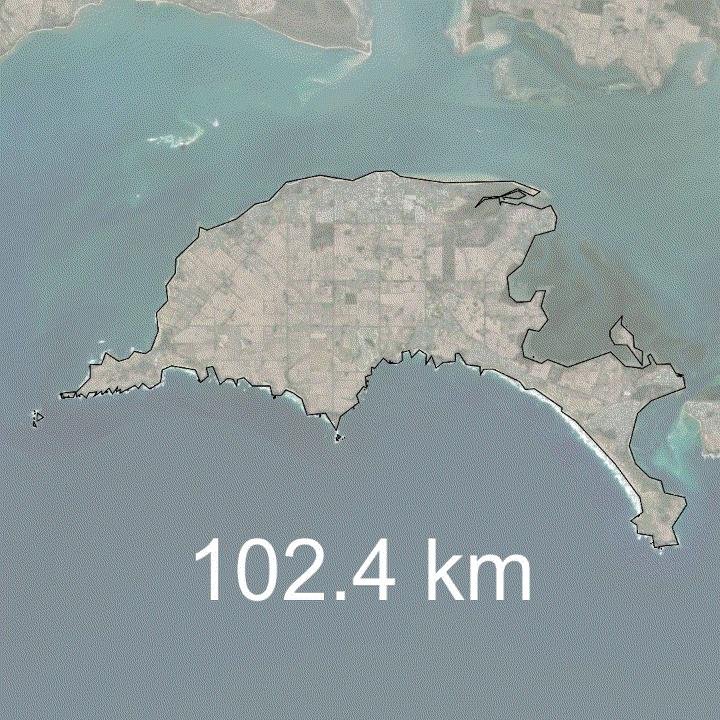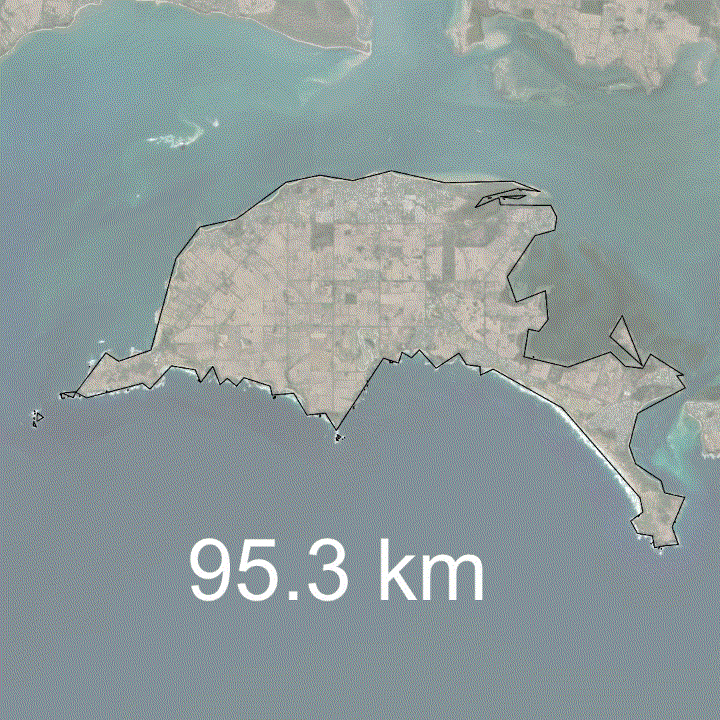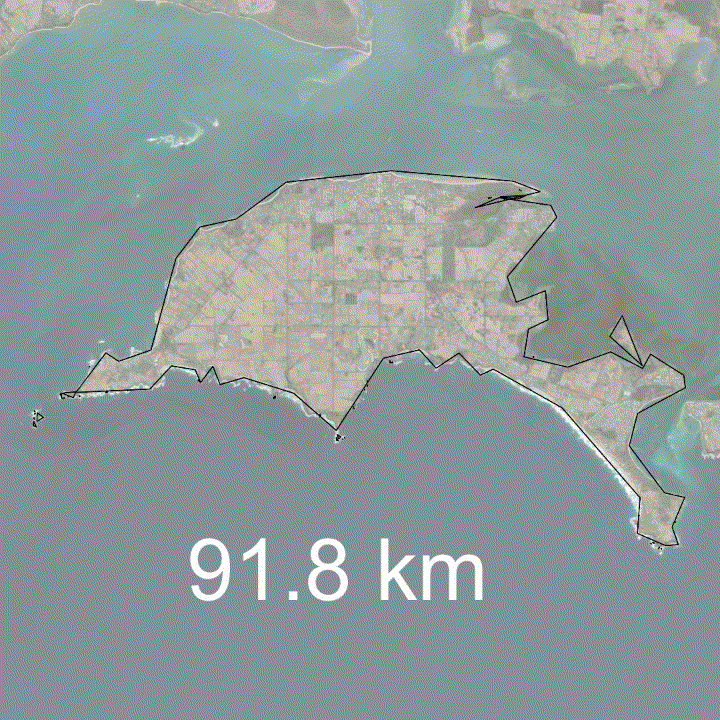
Below is an example of the coastline paradox on Phillip Island, Victoria, Australia.
In this example, you can see that the more the coastline is generalised, as would happen at larger scale maps, the coastline length decreases. Conversely, the more detailed you made the map, say, if you zoomed in on a particular bay, more detail would become obvious and the coastline length would increase.
This paradox was first identified by mathematician Lewis Fry Richardson in 1961, and has since been observed in many natural and human-made coastlines around the world.
The coastline paradox arises from the fractal nature of coastlines. Fractals are mathematical objects that exhibit self-similarity at different scales. In the case of coastlines, this means that they appear similar when viewed from different distances. For example, if we zoom in on a section of coastline, we will see smaller bays, coves, and inlets that were not visible at larger scales. These features contribute to the overall length of the coastline, as they create additional twists and turns that must be accounted for when measuring its length.
The coastline paradox has important implications for the study of geography, geology, and cartography. For example, the length of a coastline is often used as a measure of the country's size or land area, but this measure can vary significantly depending on the scale at which it is measured. Additionally, the fractal nature of coastlines can make it difficult to accurately represent them on maps or in geographic information systems (GIS). This is because maps must represent coastlines at a fixed scale, which can result in the loss of important details at smaller scales or the introduction of distortions at larger scales.
The coastline paradox has been observed in many other natural and human-made coastlines around the world. For example, the coastlines of Norway and New Zealand are particularly fractal-like, with many small bays and inlets that contribute to their overall length. In contrast, the coastlines of Australia and Antarctica are relatively smooth and less fractal-like, resulting in shorter measured lengths.
One implication of the coastline paradox is that it highlights the importance of scale in understanding complex natural phenomena. In the case of coastlines, the fractal nature of their structure means that they appear different depending on the scale at which they are viewed. This has important implications for the study of geography and geology, as it suggests that phenomena such as erosion and sedimentation may operate differently at different scales.
In conclusion, the coastline paradox is a fascinating mathematical concept that describes the counterintuitive observation that the length of a coastline depends on the scale at which it is measured. This paradox arises from the fractal nature of coastlines, which exhibit self-similarity at different scales. The coastline paradox has important implications for the study of geography, geology, and cartography, as it highlights the importance of scale in understanding complex natural phenomena. Ultimately, the coastline paradox reminds us that the world around us is complex and multifaceted, and that our understanding of it must be approached with care and attention to detail.